基本表式

絶対零度でのGreen関数について

参考文献

• Fetter Walecka

(1粒子) Green関数の定義

• :ハイゼンベルグ表示での場の演算子であり, ．
• である．
• フェルミ粒子の場の演算子には反交換関係があり. 同時刻の反交換関係であることに注意。
• は時間順序積であり, 時間の順序を左側に未来の時間, 右側に過去の時間となるように並べ変える．
• : ステップ関数 なら1, なら0である．
• :ハイゼンベルグ表示の粒子での基底状態

相互作用のない系でのGreen関数

ハミルトニアン

ハミルトニアンを として, 基底状態のエネルギーを0としておく．:フェルミエネルギー, : 粒子数演算子であり, 基底状態の粒子数をとすると. また, 相互作用がない場合は1粒子状態の和であるので

である．

WARNING

エネルギーの基準(ゼロ点)をフェルミ準位にしていることに注意．

ここで, 1粒子ハルミトニアンの固有関数を(これは完全系をつくる)として, 場の演算子を展開した係数をとしている．

相互作用のない場合の基底状態は, エネルギーをもつ占有軌道がフェルミ準位までフェルミ分布に従い占有している．

実時間表示

によって電子が非占有状態に生成されるもしくは, によって正孔が占有状態に生成される(占有状態電子を消滅する)という2通りが, それぞれGreen関数の1項目と2項目に対応する．

• 生成と消滅は同じ1粒子状態に対して行なわれる．そうでない場合はゼロになる．
• 正孔の生成状態も励起状態であり基底状態からの，励起エネルギーはである．

導出

よって,

となる。最後の行では, 電子と正孔の寄与を分けて定義しておく。これはグリーン関数と何かの積を考える際に理解の助けになる。

INFO

グリーン関数は実空間, 実時間表示で見る方がイメージしやすい．

振動数表示

Green関数はの関数なので,それについてフーリエ変換した表式も用いられる．レーマン表示とかスペクトル表示と呼ばれている． ステップ関数をフーリエ表示として

がある．ここでは正の微少量．面の下反面の留数を拾う拾わないかでステップ関数を表現している．

INFO

フーリエ変換は，規格化因子の不定性があるので，この文章では以下のようにしておきます．

のフーリエ変換を考えると, (はの中の をとすればよい)

となっているので,

を得る．複素数に拡張した面では,非占有状態(電子励起)の極がの下反面，占有状態(正孔励起)の極が上反面ににある．

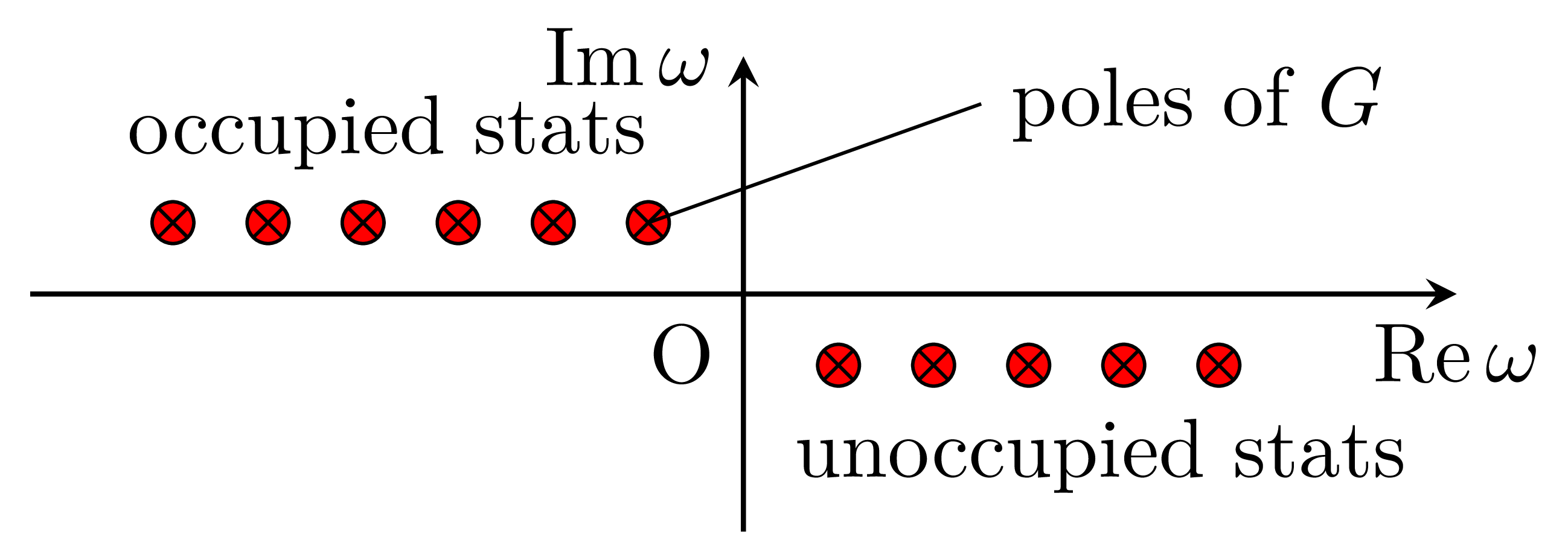
INFO

実時間表示の定義についていたは, 振動数表示での表式がキレイになるようにつけられていた．

状態密度

の関係式を用いると,

となるので形式的には状態密度は

のように書ける(や符号があっている??)

時間秩序分極関数

ハイゼンベルグ表示の密度演算子をとすると である． 密度の期待値からの変位を表す演算子としてを導入する． このとき時間秩序分極関数は以下のような時間順序積による密度の積(密度相関)と定義する．

相互作用がない系での時間秩序分極関数

相互作用がない系では、N積項は消えるためWickの定理により

となる。のように分離でき、では が残りでは が残ることを思い出すと

となる。このフーリエ変換は上記と同様に

を得る。 のように波動関数の積を展開する規格直交化する基底をとし, 展開係数をとする。 (を満たす)。 このときをでの展開係数は以下のようになる。